In the previous activity we used minimum distance classification to assign the classes of our objects. However, even with our best choice of features, relying on the distances amongst feature vectors may still be ambiguous. This was not a problem in our previous activity but such a scenario is indeed possible. In activity 14 if we had just opted to use the normalized Red value and the Area/Perimeter^2 it would have been very difficult to differentiate between heart and diamond. In this activity we implement another method of classification called Linear Discriminant Analysis (LDA). We will still be using the same feature vectors that we described in activity 14 but this time we will use a different method for calculating an object’s class.
In pattern recognition we may think of the all the events as having a given probability. Let us consider two classes and a single object. Assuming that the object and the classes have similar features we may consider that the error or accuracy of our classification is given by the probability of assigning the object to the wrong or correct class. Moreover, the probability that an object came from a given class not only depends on its features but also the knowledge of how many objects belong to a given class. LDA is simply a method of calculating the probability of an object to belong to a given class using their features. The membership of an object is decided by the class that has the highest probability of containing it. The LDA method is based on the assumption that each class has a multivariate Normal distribution and that all the classes share the same Covariance matrix.
LDA calculates the probability, fij, of an object to belong in a class according to the equation
In this equation wi is the feature vector of object i and mj is the mean feature vector of class j. The value pj is the probability or ratio of the number of elements in class j over the total population of the classes.
Matrix C is the shared covariance matrix of all the classes and is calculated as the weighted mean of all the covariance matrices, cj, of the classes. We calculate the covariance matrix of each class following equation 3, where m is the mean feature vector of all the objects in all classes and Wj is the matrix containing all the feature vectors of all the members of class j. Finally nj is the number of membership in a given class.
Using the feature vectors we obtained in activity 14 we use LDA to classify the objects into the four classes of heart, diamond, spade, and club. We used the nine training objects in activity 14 to determine the covariance matrices and mean feature vector of the classes. All the raw data we used are shown in activity 14 Table 1 and Table 2.
I give myself a grade of 10 in this activity. I want to thank Orly, Kaye, and Jaya for answering my questions.
Main Reference
Teknomo, Kardi. “Discriminant Analysis Tutorial”. http://people.revoledu.com/kardi/ tutorial/LDAKardi
In pattern recognition we may think of the all the events as having a given probability. Let us consider two classes and a single object. Assuming that the object and the classes have similar features we may consider that the error or accuracy of our classification is given by the probability of assigning the object to the wrong or correct class. Moreover, the probability that an object came from a given class not only depends on its features but also the knowledge of how many objects belong to a given class. LDA is simply a method of calculating the probability of an object to belong to a given class using their features. The membership of an object is decided by the class that has the highest probability of containing it. The LDA method is based on the assumption that each class has a multivariate Normal distribution and that all the classes share the same Covariance matrix.
LDA calculates the probability, fij, of an object to belong in a class according to the equation
In this equation wi is the feature vector of object i and mj is the mean feature vector of class j. The value pj is the probability or ratio of the number of elements in class j over the total population of the classes.
Matrix C is the shared covariance matrix of all the classes and is calculated as the weighted mean of all the covariance matrices, cj, of the classes. We calculate the covariance matrix of each class following equation 3, where m is the mean feature vector of all the objects in all classes and Wj is the matrix containing all the feature vectors of all the members of class j. Finally nj is the number of membership in a given class.
Using the feature vectors we obtained in activity 14 we use LDA to classify the objects into the four classes of heart, diamond, spade, and club. We used the nine training objects in activity 14 to determine the covariance matrices and mean feature vector of the classes. All the raw data we used are shown in activity 14 Table 1 and Table 2.
Table 1. Resulting probability of each object per class and classification results.
(click to enlarge)

The result of our classification is shown on Table 1. Again we obtain a perfect 100% classification using this set of feature vectors. We however did not implement this method on the other 140 objects we used in activity 14. Still we believe that a very high classification accuracy will result if done so.(click to enlarge)

I give myself a grade of 10 in this activity. I want to thank Orly, Kaye, and Jaya for answering my questions.
Main Reference
Teknomo, Kardi. “Discriminant Analysis Tutorial”. http://people.revoledu.com/kardi/ tutorial/LDAKardi

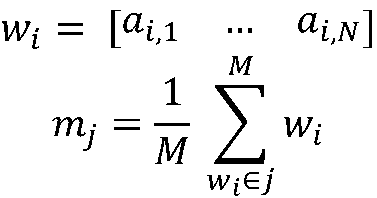

No comments:
Post a Comment