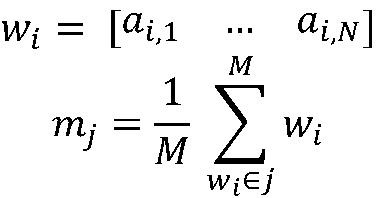Activity 17 Photometric Stereo

Many of our previous activities involved using an objects reflectance, its interaction with a light source, to do color segmentation, white balancing, and even classification. In this activity we will again use the this phenomenon to reconstruct a 3D surface. The method we will be implementing is called photometric stereo.

To give us a better understanding of our method it is best to backtrack a little. Let us consider a camera, such as those we have benn using in our previous activities. Esentially, the image obtained by a camerais simply the light intensity, I, reflected by its subject which is dependent on the materials reflectance. However aside form its reflectance this intensity pattern is also dependent on the geometry of the object which results in light and dark (shadow) areas. This is much more understood by looking at figure 1, where we can see that the reflected intensity at point P is affected by the angle at which the light hits the surface, resulting to either a bright area and/or a shadow. Hence an intesity profile of an object also contains information on its geometry. Equation 1 gives an expression for this intensity where rho is the reflectance and k is a scaling parameter.

Figure 1. Visualization of Reflection on a 3D surface

Equation 1

Looking at our model on figure 1 and equation 1, it becomes apparent that we should also take into account the type or our light source. That is, point sources, line sources, and area sources would result in different reflected intensity patterns since the light coming from them would arrive at the surface differently (different angles and intensities as a function of distance). However in this activity we limit ourselves to an approximation that our point source is at infinity which results to equation 1 having the form

Equation 2.

Since we know the intensity profile from our image, if we have information on the location of the light source we can obtain the geometry of the surface by solving for the normal vector n.

In this method, photometric stereo, we will be using multiple images of the same object but with light sources at different locations to obtain an estimate of an objects 3 dimensional geometry. Since we have images for different light source locations we can rewrite equation 2 in matrix form where each row corresponds to a image (intensity profile) light source pair. Solving for the normal vector n we obtain

Equation 3

Equation 4

We also know that this normal vector n is related to the surface c by the taking the gradient of c such that

Equation 5

Finally we obtain the surface f(x,y) by integrating

Equation 6

We implement this algorithm in Scilab and make use of matrix properties and operation to reduce the computation time.

Figure 2. Images of the surface taken with 4 different location of the light source. Their respective locations were previously provided.

Figure 2 shows the raw images we used to calculate the 3D surface. We used 4 images with sources at different locations from the matlab file photos.mat. It is easily seen from this images that indeed there is a noticeable difference with different light source position.

Figure 3. 3D plot of the calculated surface of the 3D object. Errors are seen as spikes and dips over the surface

Using the algorithm we discussed and the raw images shown in figure 2 we reconstruct a hemispherical surface shown in figure 3. The resulting surface we obtained is in good agreement with our expectation. Notice that the shape is indeed that of a sphere and the background remains flat. However we also see that the surface is very rough and there is even a gentle dip in a the shape of a cross over the hemishpere. These imperfections is inherent to our method, since it is still only an approximation. A much better result may be obtained by having more images (hence more information resulting to a better approximation). Still overall we can say that the method is a success and is fairly simple to implement.

I give myself a grade of 10 in this activity. I thank Dr. Gay Pereze for her patience and useful adice.

Main Reference

A17– Photometric Stereo by Dr. Maricor Soriano, 2008

Activity 16 Neural Networks

Do you remember when I said machines are stupid? Well, I am not the first or the only one to believe so. Genius scientists and programmers that came before us also believed that machines and computers are sorely lacking when compared to the human brain. Just like in our pattern recognition activities (14 and 15), after creating our feature vectors we still needed to implement a formula so that the computer would classify the objects. So the brilliant scientists and programmers of the 19th century developed the “Neural Network”. The “Neural Network” works by mimicking how our own brain works; that is each neuron takes in multiple weighted inputs, processes the information, and then passes its output to a succeeding neuron. A collection of many interconnected neurons forms a “Neural Network.” The main advantage of using “Neural Network” over LDA and minimum distance classification is that we do not need to apply various classification rules and formulas.

Although I said that we do not use formulas with “Neural Network”, strictly speaking we still do. However this various calculations happen or exists within the structure of the network and the user won’t ever encounter it. We use “Neural Network” by simply giving it examples of a class and telling it that that particular example is a member of a specific class. For a given amount of time or iterations the “Neural Network” will adjusts the input weights of each neuron to minimize its error (identifying an object as a member of the wrong class). After all the iterations the “Neural Network” has already “learned” and will identify an object as a member of any class it has learned.

In this activity we will use Neural Networks from the ANN toolbox of SciLab to do pattern recognition. Our input to the neural network is the feature vectors we have from activities 14 and 15. We train the neural network by giving it 9 examples of each of the 4 classes and telling it which class each object belongs to (Activity 14 Table 1). Also we test the accuracy of the “Neural Network” network by letting it classify 40 more objects, one for each class, and counting how many it classified correctly. We test the accuracy of classification for different learning rates of the “Neural Network” from 0.01 to 0.99.

Table 1. Classification result and percent accuracy at different learning rates.
(click to enlarge)

Table 1 shows the results and accuracy of classification of the “Neural Network”. We see that as expected as we increase learning rate the accuracy of classification also increases and reaches a maximum of 100% at a learning rate of 0.23 to 0.55. The red box over table 1 highlights the area with 100% accuracy. However, as we increase the learning rate beyond 0.55 the accuracy slightly decrease to 97.5%. This is not expected since a higher learning rate should result in better classification. The classification accuracy versus learning rate is plotted in figure 1 and this trend of increase and slight decrease is observed much better.

Figure 1. Classification accuracy versus Neural Network learning rate. Red line highlights range with 100% accuracy

It would have been better to do multiple trials at different seed values to determine the standard deviation of the classification accuracy for each learning rate. If we have this information we might find out that this decrease in accuracy is not significant and is within the standard deviation. It would have also been better if we explored the effect of number of learning iterations but this was not explored due to time constraints.I would like to thank Kaye for reminding me of what to do in this activity. I give myself a grade of 10.

Main Reference:
Maricor Soriano, A16 – Neural Networks, AP186 2008
Cole’s AP186 Blog

Activity 15 Probabilistic Classification

In the previous activity we used minimum distance classification to assign the classes of our objects. However, even with our best choice of features, relying on the distances amongst feature vectors may still be ambiguous. This was not a problem in our previous activity but such a scenario is indeed possible. In activity 14 if we had just opted to use the normalized Red value and the Area/Perimeter^2 it would have been very difficult to differentiate between heart and diamond. In this activity we implement another method of classification called Linear Discriminant Analysis (LDA). We will still be using the same feature vectors that we described in activity 14 but this time we will use a different method for calculating an object’s class.

In pattern recognition we may think of the all the events as having a given probability. Let us consider two classes and a single object. Assuming that the object and the classes have similar features we may consider that the error or accuracy of our classification is given by the probability of assigning the object to the wrong or correct class. Moreover, the probability that an object came from a given class not only depends on its features but also the knowledge of how many objects belong to a given class. LDA is simply a method of calculating the probability of an object to belong to a given class using their features. The membership of an object is decided by the class that has the highest probability of containing it. The LDA method is based on the assumption that each class has a multivariate Normal distribution and that all the classes share the same Covariance matrix.

LDA calculates the probability, fij, of an object to belong in a class according to the equation

Equation 1

In this equation wi is the feature vector of object i and mj is the mean feature vector of class j. The value pj is the probability or ratio of the number of elements in class j over the total population of the classes.

Equation 2

Matrix C is the shared covariance matrix of all the classes and is calculated as the weighted mean of all the covariance matrices, cj, of the classes. We calculate the covariance matrix of each class following equation 3, where m is the mean feature vector of all the objects in all classes and Wj is the matrix containing all the feature vectors of all the members of class j. Finally nj is the number of membership in a given class.

Equation 3

Using the feature vectors we obtained in activity 14 we use LDA to classify the objects into the four classes of heart, diamond, spade, and club. We used the nine training objects in activity 14 to determine the covariance matrices and mean feature vector of the classes. All the raw data we used are shown in activity 14 Table 1 and Table 2.

Table 1. Resulting probability of each object per class and classification results.
(click to enlarge)

The result of our classification is shown on Table 1. Again we obtain a perfect 100% classification using this set of feature vectors. We however did not implement this method on the other 140 objects we used in activity 14. Still we believe that a very high classification accuracy will result if done so.

I give myself a grade of 10 in this activity. I want to thank Orly, Kaye, and Jaya for answering my questions.

Main Reference
Teknomo, Kardi. “Discriminant Analysis Tutorial”. http://people.revoledu.com/kardi/ tutorial/LDAKardi

Activity 14 Pattern Recognition

Us humans already have the inborn instinct or skill that allows us to recognize or differentiate one thing from the other. And most of the time, our own observations and experiences are enough for us to learn which is which. However machines and computers do not posses this instinct (they don't have instincts); much like how we teach babies and kids, we must also exert effort to teach machines how to recognize various things it may encounter. The difficulty with machines is that, although their language is based on math, they are still much harder to teach compared to kids (machines are stupid). In spite of this, the growing demand to increase productivity through automation and the physical limitations of the human body (there is just so much our body can do) pushes us to rely on machines and computers for various tasks. This demand and need for automated machine recognition resulted to a field known as machine vision. One sub domain of machine vision is pattern recognition which, from the name implies, basically means having a machine recognize and classify/segregate objects of patterns. In this activity we will be using Scilab to do pattern recognition of objects from an image. Our method for classification we will be using is the minimum distance classification.

All pattern recognition problems start with having a set of patterns or objects with a finite number of classification groups or classes. Each group or class is differentiated from each other based on a set of identifiable features and parameters. Hence in all pattern recognition tasks the first step is selecting the parameters or features we base our differentiation from. Since we are dealing with images it is logical that we use visually obtained information as our features. These features may be, color, shape, size, area, etc. and we may use as many as we see fit. We just have to remember that we need to select features that are distinctive to our objects or patterns otherwise we wont be able to classify them. In our method we place these features into vector form. That for each object there corresponds a vector that contains all of its features (equation 1).

Equation 1

The next step is to train the computer to recognize the different patterns. In our method this simply means that for each class we select a few samples and we take the average of their feature vectors (equation 2). This mean vector serves as the representation of the whole class; that is, each class should have a unique mean feature vector.

Equation 2

The final step is to test whether our feature selection and training was sufficient. We do this by letting the computer classify the other objects (excluding those used in training). The accuracy of classification depends on how much of the objects were classified into their proper classes. The minimum distance classification, which we use in this activity works by following equation 3.

Equation 3

As in equations 1 and 2 wi is the feature vector of object i and mj is the mean feature vector of class j. Using this equation we simply calculate d for each object for each class. We then classify object i into the class that resulted in the highest value of d.

In this activity I chose the suites of playing cards as my object class. Since I don't have a camera, I scanned the cards and this served as my raw data. From this images I classified whether the pattern is heart, diamond, spade, or club. Take note that I only consider the figures as my object and not the actual playing card (in other words the 10 of spades has 10 spade objects).

Figure 1

I used three features to construct the vectors describing each object. The first feature is their normalized R value (see activity 12). As expected the R value of diamond and heart is the same and so is the value of spade and club. Diamond and heart had a very high R value whereas club and spade had a low one. This made it easy for me to segment these objects from the background (figure 1) and calculate the other features I used. However, the segmentation was still not perfect so I used closing and opening (activity 8 and 9) operations to further improve the quality.

The next 2 features I used both characterizes the shape of each object. I calculated the ratio of the total area of each object with the area of the minimum rectangle that can contain the object which served as the second feature. The area of the minimum rectangle is simply the product of the maximum dimensions of the object ([max(x)-min(x)]*[max(y)-min(y)]) The final feature was simply the ratio of the object's total area with the square of its perimeter.

Table 1. Features and Group of Training set
(click to enlarge)

Table 1 contains all the features and group classification of the 9 samples per class I used to construct the training set and the mean feature vector of each class. I also labeled each group such that grp 1 are hearts, grp 2 diamonds, grp 3 spades, and grp 4 clubs. Now using the feature vectors of the other 40 objects in figure 1 (10 per suite/class) I calculated the corresponding d for each class. Table 2 shows the result of classifying these 40 objects and we clearly see a 100% accuracy of classification. This is further highlighted in figure 2 where I plotted the feature vectors of each object. Although the plot of Area/maxDim vs R could not distinguish between heart and diamond, it was compensated by the other parameters as seen in the 3D plot (figure 2d).

Table 2. Parameters and Classification Results of the 40 Test Objects
(click to enlarge)

(click to enlarge)
Figure 2. a)Area/max Dimensions vs R, b) Area/Perimeter^2 vs R, c) Area/max Dimensions vs Area/Perimeter^2, d) 3D plot R (x axis), Area/max Dimensions (y axis), Area/Perimeter^2 (z axis). The classes heart, diamond, spade, club are represented by the red, green, blue, black markers respectively.

Having tested the accuracy of our method I further tested its flexibility using larger images with mixed objects (figure 3) with a total of 140 objects. The results shown in Table 3 and Figure 4 still shows a 100% accurate classification.

Figure 3.

Table 2. Classification Results of the 140 Test Objects in figure 3
(click to enlarge)

(click to enlarge)
Figure 4. a)Area/max Dimensions vs R, b) Area/Perimeter^2 vs R, c) Area/max Dimensions vs Area/Perimeter^2, d) 3D plot R (x axis), Area/max Dimensions (y axis), Area/Perimeter^2 (z axis).

I give myself a grade of 10 in this activity for a job well done. I would like to thank Ms. Cindy Liza Esporlas for helping me scan the cards and sending me the images. I also would like to thank Mr. Jay Samuel Combinido for teaching me to do 3D plots.

Main Reference

Maricor Soriano, A14 - Pattern Recognition, AP186 2008

Activity 13 Correcting Geometric Distortion

Have you ever tried looking through one of those door peepholes, the ones that allow you to see who is knocking on your door? I, myself, have only tried it ones when I visited my cousin who lived in a hotel and the door of their room had one. Anyway, for those of you who have tried using one, I am sure that you have also noticed that the image you see through it is highly distorted. This geometric distortion is similar to that found in some cameras (in a much lower degree) and other instruments that use spherical lenses. Basically geometric distortion results from the varying magnification as the distance from the optical axis increases. The two most common forms of this optical abberation is the barrel (magnification decreases farther from the optical axis) and pincushion distortion (magnification increases farther from the optical axis). In photography barrel distortion is commonly encountered when taking wide angle photos. In this activity we will be correcting geometrically distorted images numerically.

Figure 1. Example of distorted images

Our method of correcting geometric distortion involves two main steps. The first step is correcting the pixel coordinates, which refers to mapping the coordinates of the distorted image back to the ideal undistorted image. Our experience with image processing allows us to understand that the process of distortion simply involves the ideal undistorted image and a distorting transfer function such that

Equation 1

Where T is the transfer function and f and g are the undistorted and distorted images respectively. So given the distorted image we just need the transfer function to recover our ideal image. However the process to determine the transfer function requires us to have information on the undistorted image. Our method allows us to calculate the transfer function using only vertices of polygons or regularly occurring patterns present in our image.

Figure 2

Consider figure 2 above where we show an undistorted and distorted polygon/grid. assuming that the area of the polygon is not to large we can approximate the transformation as

Equation 2

The 8 unknown coefficients in this transformation can be solved using the for vertices of the polygon such that in matrix form

Equation 3

This resulting transfer function is valid for all points with in the polygon as long as it is not to large.

The ideal grid required in this method can easily be generated using the least distorted area in the distorted image. The dimensions of the least distorted "box" can be used to construct the ideal grid. We would then just need to determine the transfer function for each pair of distorted and undistorted "boxes." Using these transfer function we can now solve equation 2 to determine the distorted coordinates of each point in the ideal image. That is we can now determine the graylevel values for each ideal undistorted image coordinate by copying the graylevel value of its corresponding distorted coordinate. This is the second step of our correction process.

However, most of the time our calculated distorted coordinates are not integers. For such cases we need to interpolate the graylevel value for our ideal undistorted image. Three commonly used interpolation techniques are the nearest neighbor, bilinear interpolation, and cubic convolution. In this activity we choose to implement bilinear interpolation which has a much better quality than nearest neighbor and is much faster compared to cubic convolution.

Equation 4

Equation 5

Bilinear interpolation works as in equation 4. That is, the greylevel v is assigned to the coordinate (xhat,yhat). so by solving equation 4 we can obtain the gray values even for non-integer coordinates. The unknown coefficients of equation 4 can likewise be determined similar to equation 3 but know we use the four nearest pixels around (xhat,yhat) (figure 3, equation 5).

Figure 3. Visualization of Bilinear Interpolation

In this activity I used an image with barrel distortion downloaded from the internet. Figure 4 shows the original image and the ideal grid I generated using the least distorted area in the image. After implementing the method we have discussed I was able to remove the obvious barrel distortion of the image.

Figure 4. (left) Original distorted image with indication of corrected area (red box) and area of least distortion (yellow box). (center) Ideal grid generated from area of least distortion. (right and bottom) Resulting corrected image.

The result presented in figure 4 shows that our method is very effective in removing barrel distortion. It is clearly seen that the previously curved lines are now vertically and horizontally straight. The bricks that previously had different sizes are now more uniform. The only inaccuracy we can see is that some of the bricks are slightly tilted. It is hard to determine whether they should be tilted or not but I believe it is safe to assume that most of them are squarely laid-out. Still, even with this slight error, we see very promising and convincing results.

Figure 5. Corrected image with color. The red circles identify areas with erroneous color.

Figure 5 shows a colored version of our result. This was generated by implementing the correction process for the 3 color channels and combining them into one image. This colored result shows one more error. We clearly see that at some points have colors that are obviously not accurate. This is because at these points one or two of the three color components are not properly represented. Using the same reference points in all the color channels may result in some points having the wrong color component values. In other words although the gray scale result looks almost perfect it cannot be directly implemented to a colored image and expect the same level of accuracy.

I thank Ate Cherry for helping me understand the correction procedure. I give my self a grade of 10!!

Image source:
http://www.nicovandijk.net/lenses.htm

Main Reference:
A13 – Correcting Geometric Distortions by Maricor Soriano, AP186 2009